拜占庭将军问题解决的是分布式系统中含有作弊节点情况下的分布式一致性（或共识）问题。Lamport 老爷子用一组拜占庭将军商定共同攻城计划形象的描述了这个问题，这里一个拜占庭将军就指代分布式系统中的一个节点。Lamport 老爷子描述的场景大致如下：一组拜占庭将军围困了一座敌城，将军们驻扎在敌城周围，只能通过信使通信，他们必须商定一个一致的作战计划。但是，他们之间可能存在叛徒，叛徒会竭力的干扰达成计划。所以我们需要找到一个算法使那些忠诚的将军们能达成一致协议。目前的结果表明，如果将军们之间使用口头消息通信（oral message，传递过程中内容可能被更改），当且仅当超过 2/3 的将军是忠诚的时候该问题才可解，也就是说 1 个将军可以扰乱 2 个将军。如果使用不可伪造的书面信息通信，则对于任何数目的将军和潜在叛徒，该问题都是可解的。

拜占庭将军问题和 Paxos 等分布式一致性算法不同，Paxos 等算法只考虑所有节点都是可信任的情况，系统中不会出现相互矛盾的信息，而拜占庭将军问题则必须考虑系统中出现矛盾信息干扰决策情况。他们的相同点是假设消息的传输过程（信使/消息通道）是可靠的，两个节点之间传递过程中消息不会被篡改（下面有具体的定义）。

首先，我们看拜占庭将军问题的算法必须要保证达成：

A. 所有忠诚的将军达成相同的行动计划。
A. All loyal generals decide upon the same plan of action.

所有忠诚的将军会按照算法的结果去执行，而叛变将军则可以做任何他们想做的事。算法必须确保条件 A 而不管叛将们做了什么。

忠诚的将军们不应该仅仅只达成一致的协议，而且应该达成一个合理的计划。因此，我们还想确保：

B. 少数叛徒不会使忠诚的将军们采取糟糕的计划。
B. A small number of traitors cannot cause the loyal generals to adopt a bad plan.

条件 B 很难去形式化，因为它需要精确的定义何为糟糕的计划，我们不会尝试这样做。相反，我们考虑将军们如何做出决定。每个将军都会观察敌情，并将他的观察结果通告其他将军。假设 v(i) 代表第 i 个将军发送的信息，每个将军使用某些方法将值 v(1),v(2),…,v(n) 结合形成一个作战计划，这里的 n 是将军的个数。如果要使条件 A 达成，则所有的将军需要使用相同的结合方法，条件 B 达成则需要使用一个健壮（robust）方法。比如，如果只是决定是进攻还是撤退，那 v(i) 可以代表第 i 个将军觉得哪个是最好的选择（进攻还是撤退），然后基于所有将军的选择做投票的大多数做出最终抉择。这样只有在忠诚的将军两派意见差不多的情况下，少数的叛变将军才能影响最终的结果，但是这种情况下，无论是进攻还是撤退都不能算是糟糕的方案。

虽然这种方式可能不是满足条件 A 和 B 的唯一方法，但这是我们了解的唯一方法。该方法假设各位将军通过某种方法彼此传达 v(i) 值。最直接的方式是让将军 i 通过信使将 v(i) 传达给其他将军。然而，这是行不通的，因为满足条件 A 需要每位忠诚的将军获得相同的 v(1),v(2),…v(n) 值，而叛变的将军可能会向不同的将军传递不同的值。若要满足条件 A，以下条件必须成立：

\1. 每个忠诚的将军必须获得相同的信息 v (1), …, v (n)。
\1. Every loyal general must obtain the same information v (1), …, v (n).

条件 1 暗示着一个将军不一定使用直接从第 i 个将军获得的 v(i) 的值，因为叛变的第 i 个将军可能会向不同的将军发送不同的值。这意味着除非我们谨慎，否则在满足条件 1 时，我们可能会引入将军使用 v(i) 值与第 i 个将军发送的值不同的可能性，即使第 i 个将军是忠诚的。若使条件 B 能满足我们必须禁止这种情况发生。比如我们不能允许只有少数的叛徒就使得忠诚的将军们在一个个 ”retreat”, ”retreat”…… ”retreat”, 值中做决定，而每个忠诚的将军发送的明明是 ”attack”。因此，我们对每个 i 都有以下要求：

\2. 如果第 i 个将军是忠诚的，则其他的忠诚的将军必须使用他所发送的值作为 v(i) 的值。
\2. If the ith general is loyal, then the value that he sends must be used by every loyal general as the value of v (i).

我们可以将条件 1 重写为对于每个 i（无论第 i 个将军是否忠诚）的条件，

1’. 任何两名忠实的将军使用的 v(i) 值是相同的。
1’. Any two loyal generals use the same value of v(i).

条件 1’ 和 2 都是针对第 i 个将军发送的单个值的条件。因此，我们可以将考虑仅限于一个将军如何将其值传递给其他人的问题。我们用一个将军向其副将发送命令来表达这一点，从而得到以下问题。

拜占庭将军问题。一个将军给他的 n-1 个副将们发送一个命令，并且必须要满足：

IC1. 所有忠诚的副将遵守相同的命令。
IC2. 如果发令的将军是忠诚的，则每个忠诚的副将都遵守他发出的命令。
IC1. All loyal lieutenants obey the same order.
IC2. If the commanding general is loyal, then every loyal lieutenant obeys the order he sends.

条件 IC1 和 IC2 称为交互一致性（interactive consistency）条件。注意如果发令将军是忠诚的，则条件 IC2 包含了条件 IC1。然而，发令将军并不要求必须忠诚。

这样我们可以就使用拜占庭将军问题解决最初的问题，第 i 个将军发送他的 v(i) 值就可以当成发令将军发送命令“使用 v(i) 做为我的值”，其他将军则作为拜占庭将军问题中的其他副将。

不可能的解

拜占庭将军问题有一个看似简单但实则令人惊讶的事实：如果将军们只能发送口头信息，那么除非有超过三分之二的将军是忠诚的，否则该问题无解。比如，在只有三个将军情况下，只要有一个叛徒那该拜占庭将军问题就无解。口头消息是指其消息内容完全受发送人控制的消息，因此叛变的发送人可以传输任意可能的消息。这类消息就是对应计算机系统中常用的消息类型。在后面章节中，我们还会考虑带签名的书面消息类型，采用这种消息类型情况下上面的结论不再成立。

我们来看下为什么使用口头消息情况下三位将军中有一位叛变，该问题就无解。为了简单起见，我们考虑只能做出“进攻”和“撤退”决定的情况。如图 1 所示，发令将军是忠诚的，并给副将 1，2 发送“进攻”命令，但副将 2 是叛徒，他告诉副将 1 他从发令将军那里收到了“撤退”命令。为了使 IC2 条件（可能）能够满足，副将 1 只能执行“进攻”命令（试想如果 1 不执行进攻命令/即不遵守发令将军发送的命令，则 IC2 肯定不会满足）。

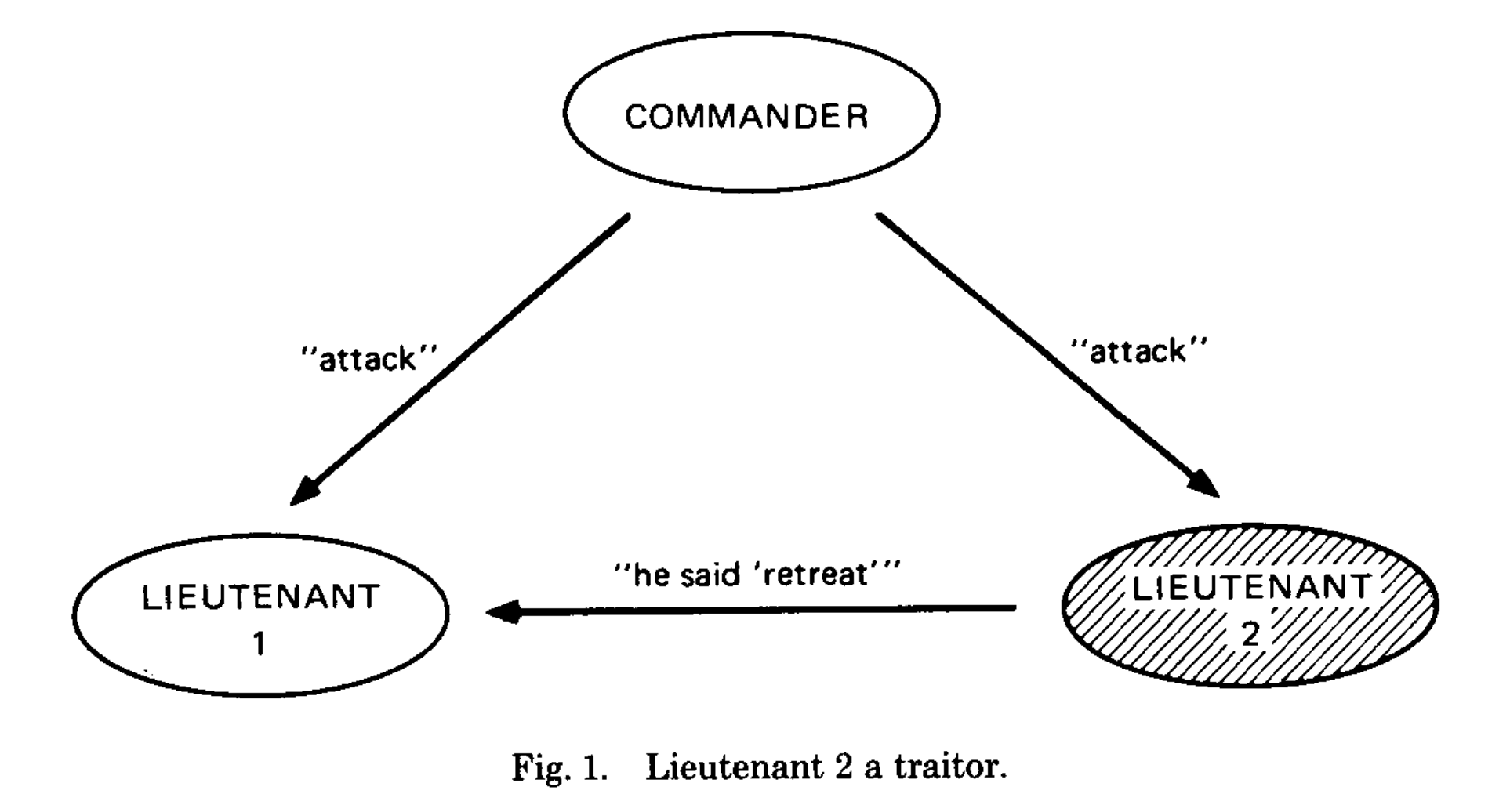
再看另外一种情况，如图 2 所示，其中发令将军是叛徒，并向副将 1 发送了“进攻”命令，向副将 2 发送了“撤退”命令，副将 2 转告副将 1 说他收到的是“撤退”命令。副将 1 不知道谁是叛徒，因此，这两张图片场景站在副将 1 的视角来看是一模一样的。副将 1 无法区分这两种情况，因此，每当副将 1 收到发令将军的“进攻”命令时，他都必须服从该命令。

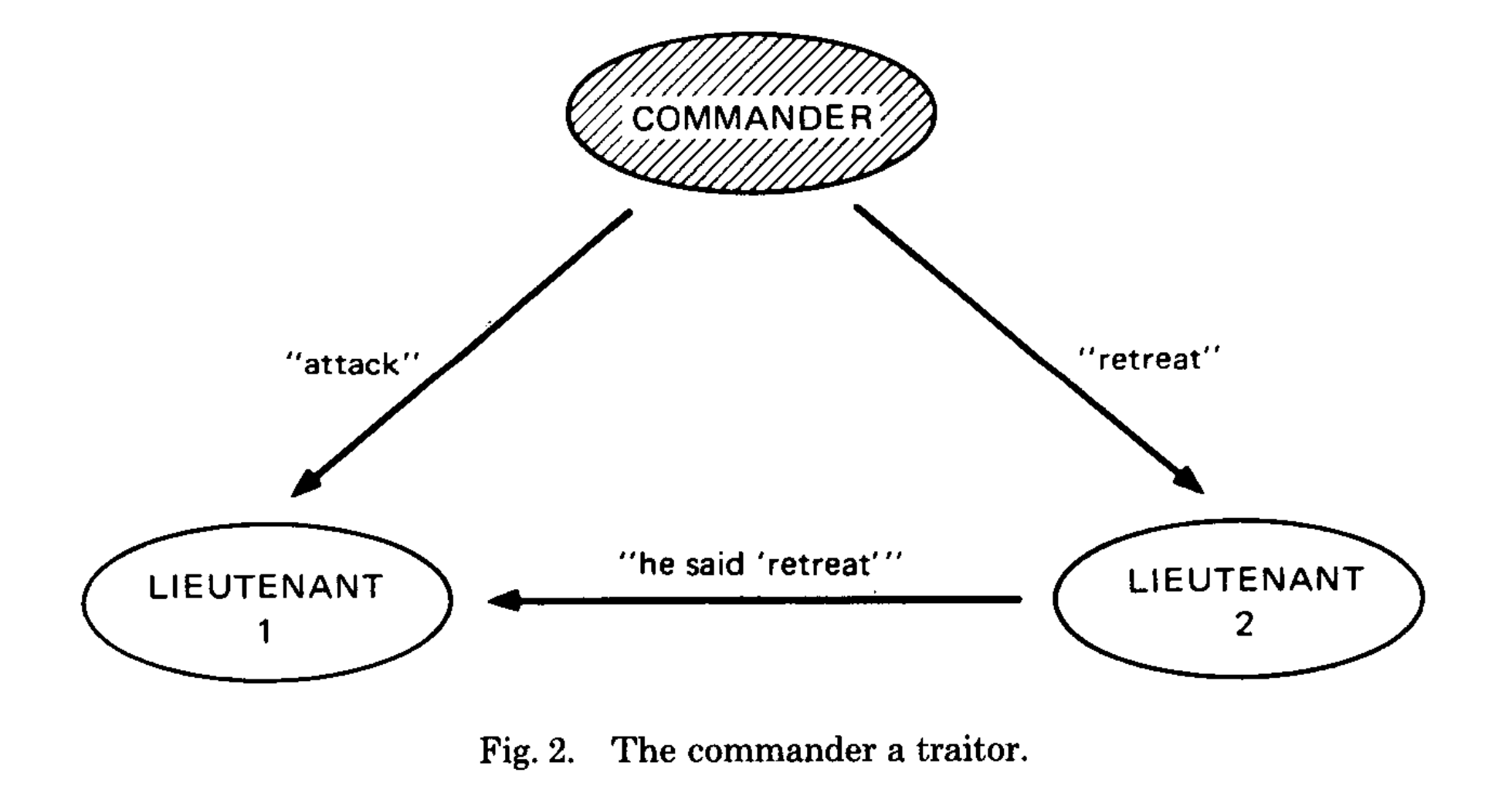
与此同理，副将 2 从发令将军那里收到了“撤退”命令，即使副将 1 告诉他发令将军说的是“进攻”，他也必须服从自己收到的命令。因此，在图 2 中，副将 1 必须服从“进攻”命令，而副将 2 必须服从“撤退”命令，从而违反条件 IC1。因此，对于存在一位叛徒的三将军问题来说，不存在任何解决方案。

口头消息的解决方案

通过上述我们可知，使用口头消息的情况下，如果有 m 名叛徒的拜占庭将军问题想要有解，则至少需要有 3m + 1 名将军。现在，我们提供一种适用于 3m + 1 个或更多将军的解决方案。但是，我们首先必须准确地限定“口头信息”的含义：

A1. 发送的每条消息均正确传递。
A2. 消息接收者能知道是谁发送给他。
A3. 消息如果丢失则可以被检测到。
A1. Every message that is sent is delivered correctly.
A2. The receiver of a message knows who sent it.
A3. The absence of a message can be detected.

A1 - A3 的限定避免了两个将军交流过程中叛徒的干扰（在实际系统中也可实现）。且目前介绍的算法要求每个将军都能够直接将消息发送给其他将军。在论文第 5 节中，还介绍了没有此要求的算法（此处略）。

如果发令将军是叛徒，他也可以选择不发送任何命令，这种情况下我们默认副将们遵守默认命令“撤退”（RETREAT）。

算法中还假设了一个函数 majority，如果有一个多数的值 v 存在，则 majority(v1,v2…vn-1) = v，否则 majority(v1,v2…vn-1) = RETREAT。我们用发送/接收某个值来代替发送/接收命令。

算法 OM(0)。（Algorithm OM(0).）
1）发令将军将其值发送给每个副将。
2）每个副将都使用他从发令将军那里获得的值，如果没有收到，则使用默认值 RETREAT。

算法 OM(m), m > 0。（Algorithm OM(m), m > 0.）
1）发令将军将其值发送给每个副将。
2）对于第 i 个副将，将其收到的值（没收到情况下为 RETREAT）设置为 v(i)，接着，第 i 个副将作为发令将军，在 OM(m-1) 轮算法中给其他 n-2 个副将发送 v(i) 里的值。
3）对于第 i 个副将，将在 OM(m-1) 轮算法中收到的其他第 j 个副将的值（同样没有则为 RETREAT）设置为 v(j) 。然后使用 majority(v1,v2…vn-1) 确定 v 值。

算法 OM(m)（Algorithm OM(m). ）中的 m 指代算法最多可以容许有多少个叛徒。不是要求有 m 个叛徒，或者已知 m 个叛徒。OM(0) 即为不提防任何叛徒的情况。

在 m > 0 的情况下，每个副将都无法信任任何人，因此对于每个接收到的值，他们都需要使用 majority(v1,v2…vn-1) 确定。在第 m 轮中，发令将军给每个副将都发送了一个值，但谁都不敢相信这个值。因此每个副将都给其他 n-2 （除消息上游和自己）个副将发送自己接收到的信息以帮助他人做决定（叛徒可以发送任何值，但规定了遵守此规则），这就是 m-1 轮。而 m-1 轮收到的值大家又需要其他人的信息做决定，因此又给其他 n-3 （除消息上游上上游和自己）个副将发送自己的信息帮助他人做决定。。。以此类推，一直到 OM(0) 为止。

上面整个过程是一个递归的过程，每个副将都会给其他副将发送很多信息，为了使这些不同信息得以区分，每个副将可以在发送消息时加上自己所属序号的前缀。此部分具体实现可进一步参考（https://www.zhihu.com/question/23167269/answer/366474865）这个回答。

OM(m) 算法证明过程，略。

使用签名消息的解决方案

从前面图 1 和图 2 的场景可以看出，叛徒的撒谎能力使拜占庭将军问题变得如此困难。如果我们可以限制这种能力，这个问题将变得容易解决。一种方法是允许将军发送不可伪造的签名消息。更准确的说，是我们给 A1-A3 加上如下的假设：

A4 (a) 一个忠诚的将军的签名不可以被伪造，且他签署的消息任何内容更改都可以被检测到。
     (b) 任何人都可以验证某个将军签名的真实性。
A4 (a) A loyal general’s signature cannot be forged, and any alteration of the contents of his signed messages can be detected.
     (b) Anyone can verify the authenticity of a general’s signature.

我们不对叛变将军的签名做限制。也即我们允许他的签名被另一个叛徒伪造，从而允许叛徒之间勾结。引入签名消息后，之前所说的限制就不存在了，对于任意叛徒的任意将军数都有可行解。

签名消息算法假设有一个函数 choice，用来从一组命令中挑选出其中一个命令。该函数唯一的要求是：1.如果集合 V 由单个元素 v 组成，则 choice(V) = v。2. 如果 V 是空集合，则 choice(V) = RETREAT。

在以下算法中，我们让 x:i 表示由将军 i 签名的值 x。因此，v:j:i 表示先由 j 对 v 值签名，再由 i 对值v:j 签名。我们让将军 0 成为发令将军。在该算法中，每个副将 i 都维护一个集合 Vi，其中包含他到目前为止收到的一组正确签名的命令。（如果发令将军是忠诚的，则此集合绝不可能包含多于一个元素。）不过不要将 Vi（收到的命令集）与副将收到的消息集混淆。很多不同的消息里面可能包含相同的命令。

算法 SM(m)。（Algorithm SM(m). ）
首先将 Vi 集合初始化为空集。
1）发令将军签署并发送他的值给每个副将。
2）对于第 i 个副将：
    A）如果他从发令将军处收到了 v:0 形式的消息，且他尚未接收过任何命令，则他 1. 设置 Vi 为 {v}；2. 发送 v:0:i 消息给所有其他副将。
    B）如果他收到形如 v:0:j1:…:jk 的消息，并且值 v 不在集合 Vi 中，则他 1. 将值 v 添加至 Vi；2. 如果 k < m，将消息 v:0:j1:…:jk:i 发送至所有序号不是 j1,…,jk 的其他副将。
3）对于第 i 个副将：当他不会再收到任何消息时，通过 choice(Vi) 选择出命令。

注意在第 2）步中，第 i 个将军会忽略任何包含的命令 v 已在集合 Vi 中的消息。且也会忽略任何格式或签名不对的消息。对于第 3）步我们没有指明一个副将如何判断他不会再收到消息。通过对 k 的归纳，很容易表明，对于每个 k <=m 的副将序列 j1,…,jk，一个副将在第 2）步中最多只会收到 1 条形如 v:0:j1:…:jk 的消息（k 超过 m 后就没必要再发送消息）。我们只要要求 jk 副将要么发送此类型消息（k < m）或者发一条消息告诉其他人他不会再发送此类的消息，这样我们就可以判断是否所有消息都已经接收（由于 A3 限定，如果一个 jk 叛徒选择两种消息都不发送那也是可以检测到的）。

下图 5 展示了算法 SM(1) 在总共 3 个将军且发令将军是叛徒情况下的消息处理流程：

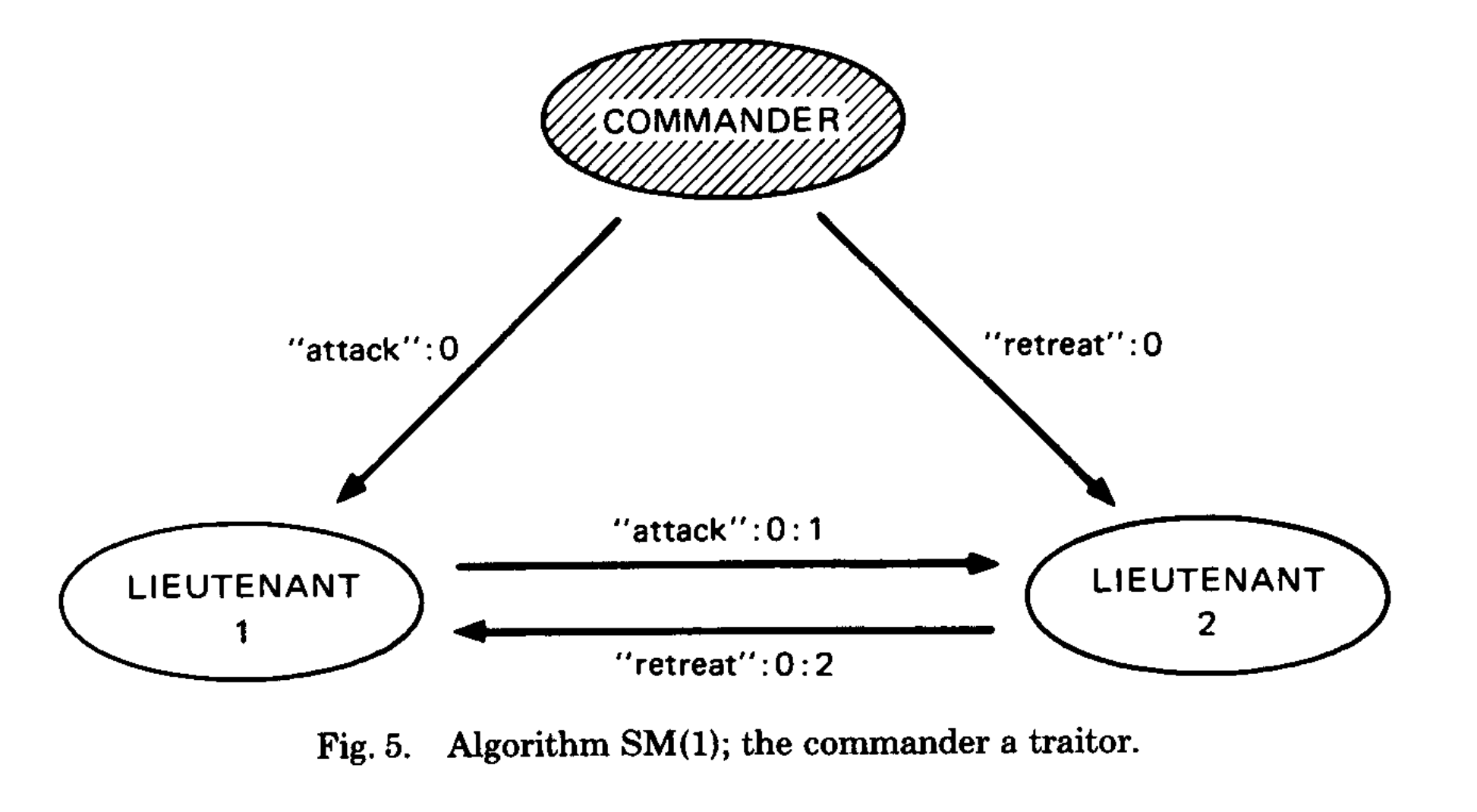
发令将军发送”进攻“命令给副将 1，发送”撤退“命令给副将 2。在第 2）步中，他们又把各自命令发送给对方。因此第 2）步之后 V1 = V2 = {”进攻“，”撤退“}，副将 1，2 都遵循命令 choice({”进攻“，”撤退“})。这里可以观察到，不像之前图 2 中的场景，副将们可以知道发令将军是叛徒，因为他的签名出现在了两个不同命令当中。

签名消息算法正确性的证明，略。

参考资料：
[1]. The Byzantine Generals Problem
[2]. 分布式理论(1):The Byzantine General Problem(译). by duanple
[3]. https://www.zhihu.com/question/23167269/answer/366474865